Summary of my Capstone Project on Orbits and the Program I Developed

My initial interest in orbits evolved from my interest in studying higher dimensions. This interest led me to a forum on higher dimensions which discussed orbits in higher dimensional orbits. For example, gravity drops off with \( \frac{1}{r^{(dimensions-1)}} \), so with higher dimensions gravity weakens more rapidly over distances. This situation creates unstable orbits in 4 dimensions or more. I discovered that orbits can be stable in 4-dimensions only if the orbit is a perfect circle. Any other orbit will spiral in or spiral out.

As I explored this more I found a site that would help me with modeling the inverse force law \( \frac{1}{r^x} \) , with any value of \( x \). I discovered that I could create more interesting force laws that use \( \cos 𝑥 \), \( \sin 𝑥 \), and \( e^x \), some of which create flower or star-shaped orbits. Also, I could change the mass of the orbiting object and central object resulting in some interesting orbits, such as the orbit of Pluto and Charon in our solar system.

I wanted to explore some additional functions that I could not incorporate into the website program, so I developed my own program which ran on Excel. This took some time and much work; however, I finally perfected it. This allowed me to utilize a Bessely function to devise a stable orbit in a 4-dimensional system. Also, I varied the mass of the two objects to see how that would impact the orbit.

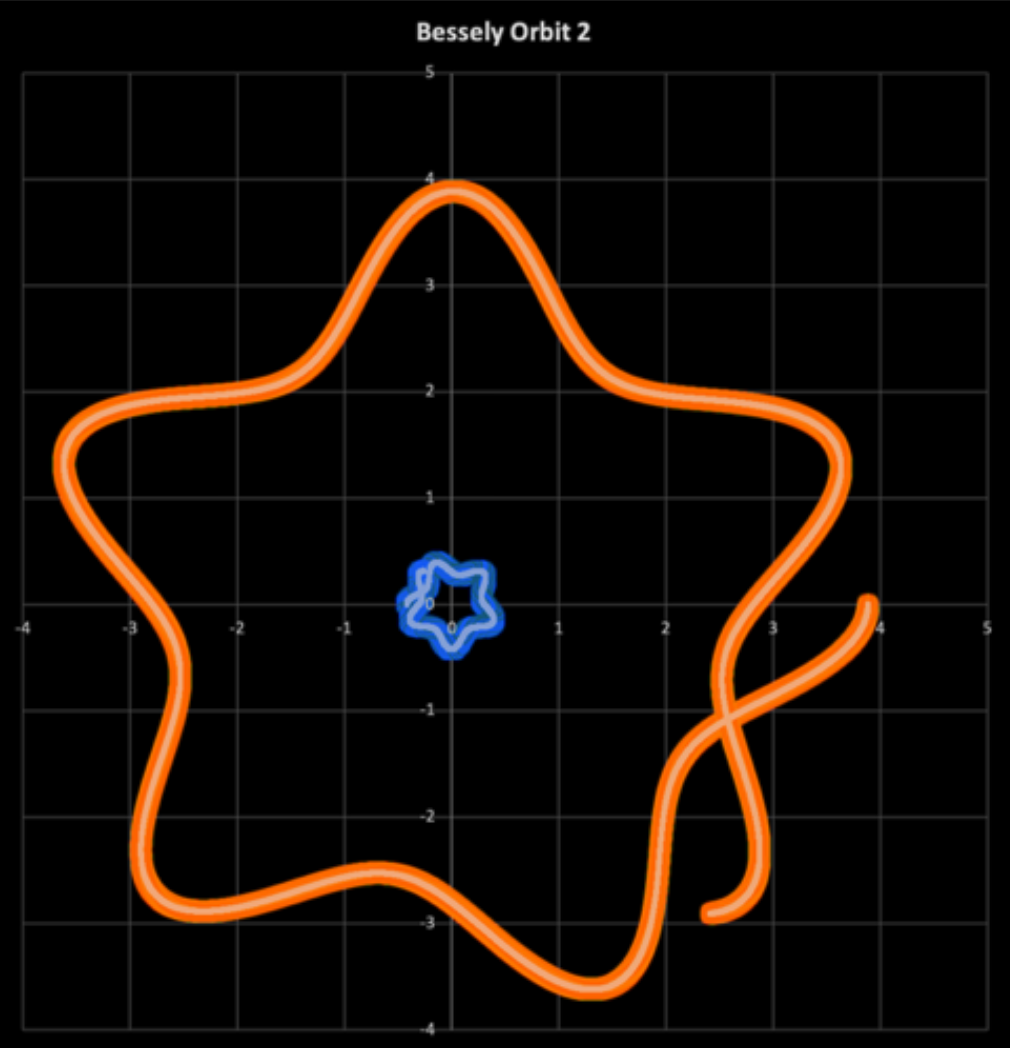
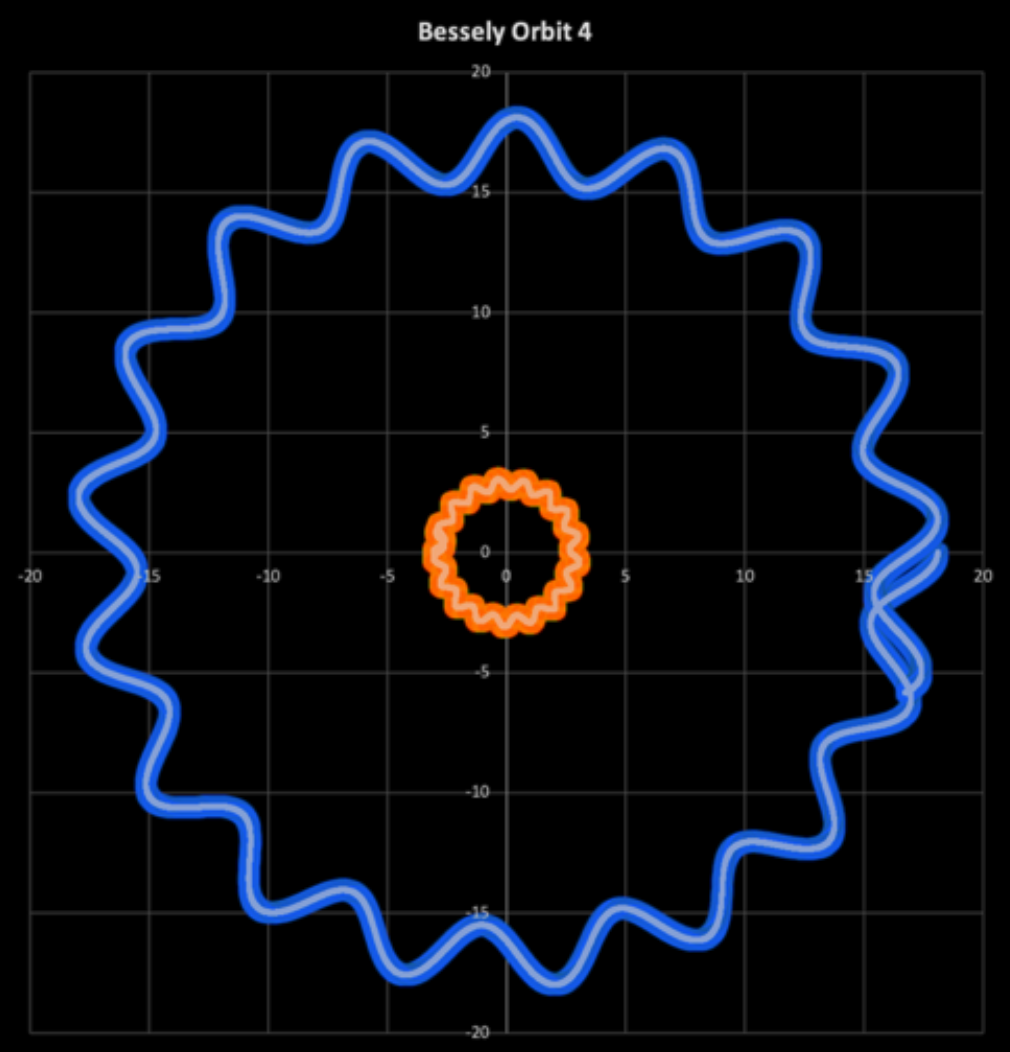
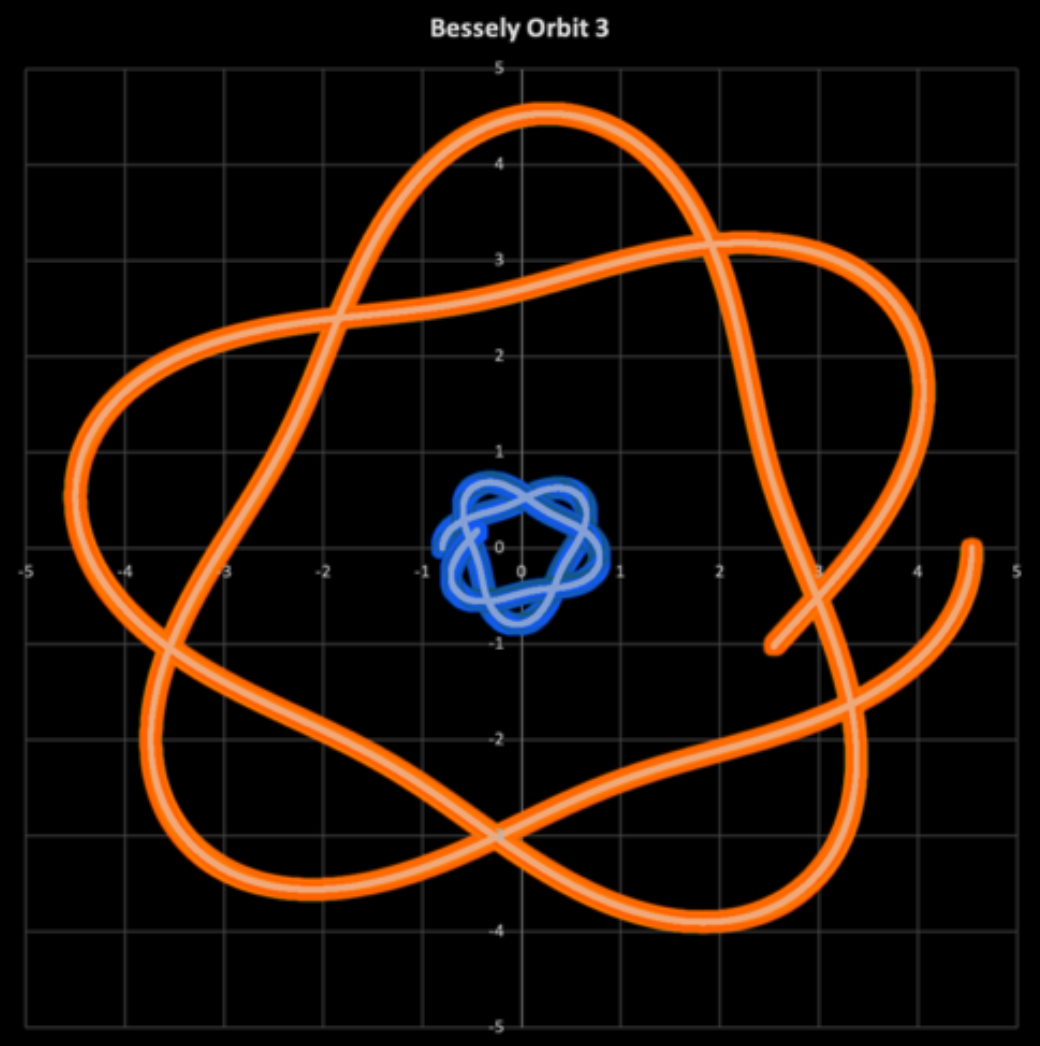
The Chair of the Math & Physics Department at Queens University of Charlotte, Michael Tarabek, Ph.D., encouraged me to utilize my interest in orbits for my senior capstone project. I still enjoy working on modeling orbits. I am also currently working on learning about modeling geodesics on a curved surface. See the link to view my capstone project.